Reversing – 799 pts (5 solves) – Chall author: k3v1n
Math lock created in Desmos. Reversable through mathematical investigation.
Challenge
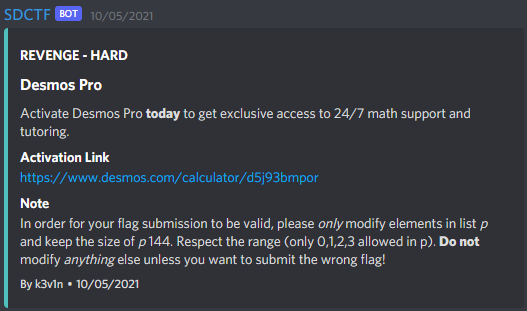
We are linked to an online Desmos file (see link above), where we are greeted by a red square. If we are able to turn the red square to green, we are able to retrieve the flag.
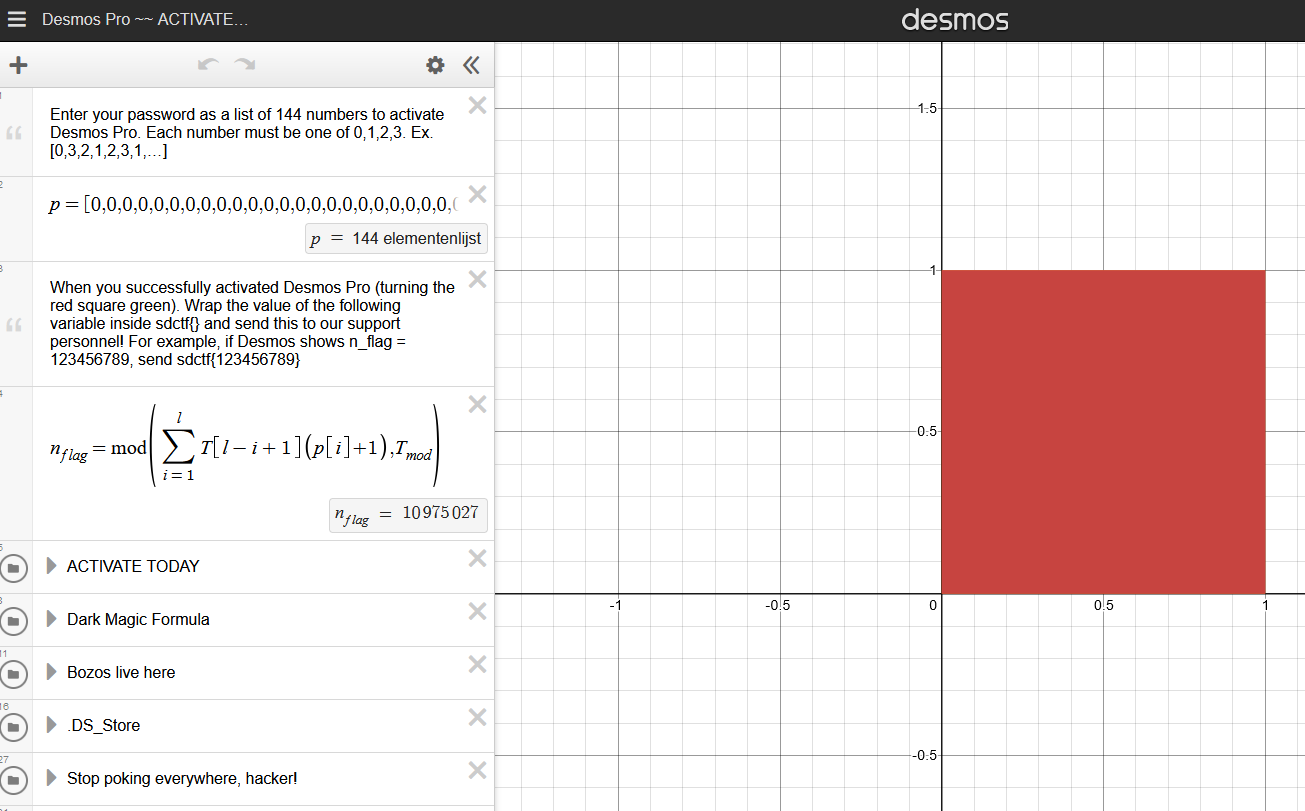
Solution
Upon inspection we find that in order to turn the square green we need to find the correct sequence p, consisting of 144 elements in {0,1,2,3}. Clearly not brute-forcable :c.
The criteria for the colouring of the square reveal that we need to find p such that C=0,
C=\left|X\left(l\right)-x_{f}\right|+\left|Y\left(l\right)-y_{f}\right|+\sum_{j=0}^{l}M\left(g\left(0,X\left(j\right),x_{max}-1\right),g\left(0,Y\left(j\right),y_{max}-1\right)\right)
From the above we can see that all three elements have to be zero in order for C to become zero. The first element, with the X function, implies that our p sequence needs to have 10 more 1’s than 3’s, whereas the second element, with the Y function, implies that our p sequence needs to have 10 more 2’s than 0’s. However, this on its own is still not enough to start brute-forcing our way through. The trick to this challenge is to understand the third element, the scary looking sum. For the sum to be zero, all individual call to M should return zero as it can only return 0 or 1. Interestingly, we note that M is dependent on sequential calls of X and Y, hence the order of p seems to matter too.
Knowing all of this, we can set-up a plan. Let us try to investigate the possible outcomes of M given values of X and Y. We know that it starts of with l=0, so X=0 and Y=20, and ends with l=144, so X=10 and Y=10. When we plot M as a function of both X and Y outputs we find some kind of maze!

Like mentioned before, we start at X=0, Y=20 (green dot) and need to end up at X=10, Y=10 (red dot) in 144 steps. Through testing with the X and Y functions we find that the values of p correspond to moving through the maze in a certain direction following 0: right, 1: down, 2: left, 3: up. We can now find our solution sequence of p to be
[2,2,1,1,0,0,1,1,2,2,1,1,0,0,1,1,1,1,2,2,3,3,2,2,2,2,3,3,3,3,3,3,2,2,2,2,2,2,3,3,2,2,1,1,2,2,2,2,1,1,2,2,1,1,1,1,0,0,0,0,0,0,1,1,0,0,3,3,0,0,0,0,1,1,0,0,0,0,1,1,2,2,1,1,1,1,0,0,1,1,2,2,2,2,3,3,2,2,1,1,2,2,1,1,2,2,2,2,2,2,2,2,3,3,0,0,0,0,0,0,3,3,2,2,2,2,2,2,3,3,3,3,0,0,0,0,0,0,0,0,0,0,3,3]
from which we retrieve our flag to be
sdctf{440778777}
Ta-da!