K3RN3LCTF 2021 - Tick Tock

Cryptography – 496 pts (6 solves) – Chall author: Polymero (me)

“I chopped up my flag and hid it behind this simple key exchange. Try dlogging your way in if you are brave enough!”

Files: ticktock.py, output.txt

This challenge was part of our very first CTF, K3RN3LCTF 2021.

Exploration

We are provided eight encrypted snippets of the flag together with the source code. Here we find an encryption class with mathematics that seem similar to Elliptic Curve Cryptography.

# TickTock class
class TickTock:
    def __init__(self, x, y, P):
        self.x = x
        self.y = y
        self.P = P
        assert self.is_on_curve()
        
    def __repr__(self):
        return '({}, {}) over {}'.format(self.x, self.y, self.P)

    def __eq__(self, other):
        return self.x == other.x and self.y == other.y and self.P == other.P
        
    def is_on_curve(self):
        return (self.x*self.x + self.y*self.y) % self.P == 1
    
    def add(self, other):
        assert self.P == other.P
        x3 = (self.x * other.y + self.y * other.x) % self.P
        y3 = (self.y * other.y - self.x * other.x) % self.P
        return self.__class__(x3, y3, self.P)
    
    def mult(self, k):
        ret = self.__class__(0, 1, self.P)
        base = self.__class__(self.x, self.y, self.P)
        while k:
            if k & 1:
                ret = ret.add(base)
            base = base.add(base)
            k >>= 1
        return ret

def lift_x(x, P, ybit=0):
    y = modular_sqrt((1 - x*x) % P, P)
    if ybit:
        y = (-y) % P
    return TickTock(x, y, P)

For each of the eight flag snippets, both a domain and two secret keys are created to conduct a key exchange with. The domain parameters, the two public keys, and the encrypted flag snippets are logged. Since we are not provided any additional information this would suggest we should be looking for a way to recover the secret keys from the public keys through solving the discrete logarithm problem.

def domain_gen(bits):
    while True:
        q = getPrime(bits)
        if isPrime(4*q + 1):
            P = 4*q + 1
            break
    while True:
        i = randint(2, P)
        try:
            G = lift_x(i, P)
            G = G.mult(4)
            break
        except: continue
    return P, G

def key_gen():
    sk = randint(2, P-1)
    pk = G.mult(sk)
    return sk, pk

def key_derivation(point):
    dig1 = sha256(b'x::' + str(point).encode()).digest() 
    dig2 = sha256(b'y::' + str(point).encode()).digest() 
    return sha256(dig1 + dig2 + b'::key_derivation').digest()


# Challenge
flagbits = [FLAG[i:i+len(FLAG)//8] for i in range(0,len(FLAG),len(FLAG)//8)]

for i in range(8):

    print('# Exchange {}:'.format(i+1))

    P, G = domain_gen(48)

    print('\nP =', P)
    print('G = ({}, {})'.format(G.x, G.y))

    alice_sk, alice_pk = key_gen()
    bobby_sk, bobby_pk = key_gen()

    assert alice_pk.mult(bobby_sk) == bobby_pk.mult(alice_sk)

    print('\nA_pk = ({}, {})'.format(alice_pk.x, alice_pk.y))
    print('B_pk = ({}, {})'.format(bobby_pk.x, bobby_pk.y))

    key = key_derivation(alice_pk.mult(bobby_sk))
    cip = AES.new(key=key, mode=AES.MODE_CBC)
    enc = cip.iv + cip.encrypt(pad(flagbits[i], 16))

    print('\nflagbit_{} = "{}"'.format(i+1, enc.hex()))
    print('\n\n\n')

# Exchange 1:

P = 900301549573709
G = (536441147308213, 433384189616311)

A_pk = (570766843177947, 254987309185033)
B_pk = (359695429521403, 51578333245862)

flagbit_1 = "6a9517c4a5b9682676d014981651fbbdbd8b950cd5f3327c5dc2c733f0bad4d8"



# Exchange 2:

P = 935680375008173
G = (752891243015718, 8106553512)

A_pk = (195456786203512, 260171210284077)
B_pk = (899265030352476, 108212548527393)

flagbit_2 = "ae98c526091bf8bcafab28527ce8ded895797048ec479cee35cd77d813116d86"



# Exchange 3:

P = 1055640765880517
G = (397997065626885, 489936393193239)

A_pk = (598336533181897, 679327572764649)
B_pk = (68569414205977, 307720608649637)

flagbit_3 = "8860b181e0b91e5af755c64761283a16c8d9d5eee81c7cafa5d6810cc5896968"



# Exchange 4:

P = 1080464169080837
G = (260443033023298, 803002953398154)

A_pk = (262506876458655, 717524579730657)
B_pk = (905505250440203, 719592813122849)

flagbit_4 = "394838402833e08299616048757c60dad287f74c8a27f2ad778ce57fdda41e41"



# Exchange 5:

P = 719079145687493
G = (498571724307025, 703949890793665)

A_pk = (498097615872285, 458905235855936)
B_pk = (596932104967, 584657608387075)

flagbit_5 = "d64cd85f564b7394e6e9e2f59e10dbdf1780aa63a990bf3d685d7fad3d3afd15"



# Exchange 6:

P = 621751256871989
G = (103410561193784, 578146374890578)

A_pk = (64283605936890, 59578661917638)
B_pk = (137204988087827, 594329296794969)

flagbit_6 = "7c36b9779171251f34769955540837b1e913020b12e9fc418ffd7d654f9a1311"



# Exchange 7:

P = 813572541888629
G = (501548042112115, 51270153549450)

A_pk = (347207896856151, 99243054278463)
B_pk = (328307503789242, 154256166661670)

flagbit_7 = "0cc396078e17d21817d580cb90c380c584d4d5bc9d026868b9e4bc8e51364c95"



# Exchange 8:

P = 1114531327051853
G = (848718170467503, 890387510936812)

A_pk = (249185531830039, 1012351003599815)
B_pk = (800057076995001, 999843105025038)

flagbit_8 = "f044e34c66a93c35f612a8f949d5add77ff434e288139cda3573814b49229ab8"

Exploitation

The first step on our way to crack this encryption it to understand what is going on. This would be rather difficult only given the additional and multiplication functions, however there is also a function that validates points called is_on_curve().

def is_on_curve(self):
        return (self.x*self.x + self.y*self.y) % self.P == 1

From this we can easily recognise the formula for the well-known unit circle (mod $P$).

Now that we have the curve, what does the point addition look like? The simplest addition rule would be that of angle addition, see the figure below (source). Take two points and their sum would be the point at the summed angle of the two points. More specifically, the angle with respect to $(0,1)$ as can be seen by the base point in the multiplication function. This group is also referred to as the ‘Clock Group’ over a prime $P$.

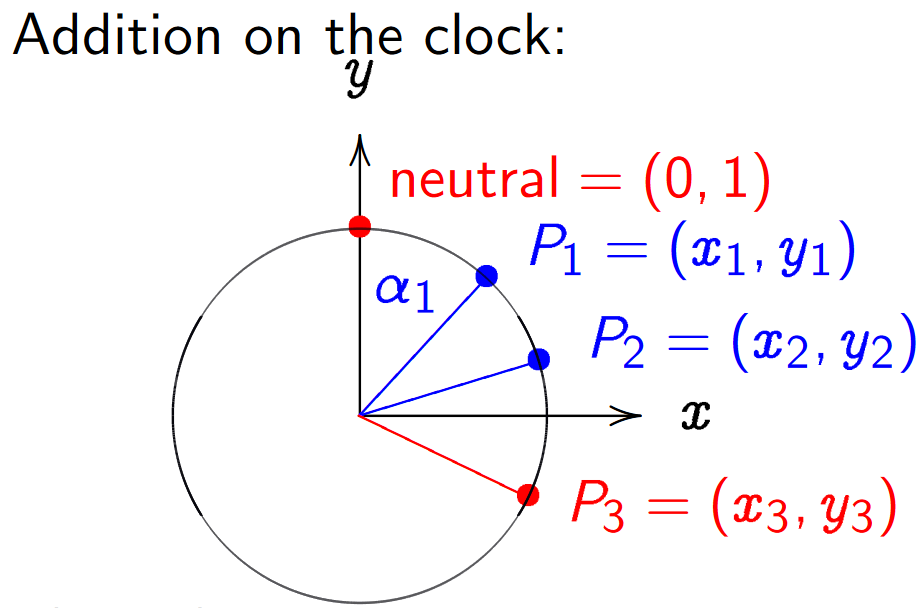
To find the addition law of two points we can consider the parametrisation

such that we can rewrite the addition of

to

Using the sine and cosine angle addition rules we can expand the above to

such that we can finally substitute the original point values back in to end up with our addition rule

Now, how to actually solve this? Brute-forcing the answer should not be easily possible due to the used prime sizes. Additionally, it is unlikely all eight primes have some underlying weakness, such as a smooth order. I could have easily prevented this during the generation of the primes, but I did not for no reason really… Turns out somebody (literally ‘somebody’) wrote an implementation of the baby-step giant-step (BSGS) algorithm in C++, which was able to solve the eight discrete logarithms in a reasonable time. However, there is a clever way to defeat this silly clock group! Let’s consider the addition rule for two equivalent points.

This should look familiar to you. Turns out it is equivalent to squaring a complex integer of the form

where $ i = \sqrt{-1} \mod{P} $. In fact, this holds for any multiple of a point. We have just found ourselves a group homomorphism!

We can use the above to map our discrete logarithms from the clock group to the multiplicative group as such

which Sage eats for breakfast! Mhuahahaha.

def solve_dlog(base, result, mod):

    ji = modular_sqrt(P-1, P)

    q  = (result.x * ji + result.y) % P
    g  = (  base.x * ji +   base.y) % P

    dlog1 = discrete_log(P, q, g)

    possibles_1 = list(range(dlog1, P, (P-1)//4))

    for k in possibles_1:
        if base.mult(k) == result:
            return k, '1'

    return 'ERROR -- DLOG not found.', '0'

Ta-da!

flag{c0m1ng_up_w1th_4_g00d_fl4g_1s_qu1t3_d1ff1cult_und3r_4ll_th1s_t1m3_pr3ssur3}

Thanks for reading! <3

~ Polymero